Specification Errors In Regression Models

Model specification errors can substantially affect the estimate of regression coefficients. The regression coefficient when measurement errors are absent.

Lecture 9 Model Specification Youtube

To sum up in developing an empirical model one is likely to commit one or more of the following specification errors.

Specification errors in regression models. This regression suggests that as class size increases the academic performance increases. The purpose of this months article is to show how specification of different models to the same data can lead to meaningful differences in the. Form imposed on the data eg.

However model specification error or model misspecification can also refer to the model. Roughly 95 of the observation should fall within - two standard error of the regression which is a quick approximation of a 95 prediction interval. For example sometimes non-normality of the residuals is solved by adding a missed covariate or interaction term.

In the first we misspecify a model by including in the regression equation an independent variable that is theoretically irrelevant. If the original model 92 satisfies MLR4 then no nonlinear functions of the independent variables should be sig-. In contrast standard regression models assume that those regressors have been measured exactly or observed without error.

I Recall the full and reduced models we have talked about when we rst introduced multiple linear regression. I Now lets revisit this issue from another perspective. T e s t S c o r e 6860 87 110 043 s i z e 0650 0031 e n g l i s h.

The standard error of the regression is particularly useful because it can be used to assess the precision of predictions. A linear regression model will include choosing the independent variables and defining the omitted variables as well as choosing the functional form. Specification error often but not always causes other assumptions to fail.

So the first step in solving problems with other assumptions is usually not to jump to transformations or some other complicated modeling but to reassess the predictors youve put into the model. To keep the discussion simple we will answer this question in the context of the three-variable model and consider in this section the first two types of specification errors discussed earlier namely 1 underfitting a model that is omitting relevant variables and 2 overfitting a model that is including unnecessary variables. Y 0 1X 1 2X 2 For some reason such as unavailability of the data on X 2 we construct a regression model without the.

Before we publish results saying that increased class size is associated with higher academic performance lets check the model specification. Such a regression model can be used with caution for prediction of the response but should not be. A common source of model specification error in OLS regressions is the omission of relevant variables.

It is understood in the regression analysis that only correct and important explanatory variables appear in the model. The idea behind RESET is fairly simple. CIt helps in the detection of heteroskedasticity when the functional form of the model is correctly specified.

DIt helps in the detection of multicollinearity among the independent variables in a regression model. When variables are omitted variations in the dependent variable may be falsely attributed to the included variables. In the second we misspecify the model by excluding from the regression equation anindependent variable that is theoretically relevant.

Specification Measurement Errors These types of errors occur when developing a linear regression model. Specification error occurs when the functional form or the choice of independent variables poorly represent relevant aspects of the true data-generating process. Specification Error is defined as a situation where one or more key feature variable or assumption of a statistical model is not correct.

Analysis We consider the first two types of specification errors discussed earlier namely 1underfitting a model that is omitting relevant variables and 2 overfitting a model that is including unnecessary variables. When the measurement errors are present in the data the same OLSE becomes biased as well as inconsistent estimator of regression coefficients. The complete regression analysis depends on the explanatory variables present in the model.

Entering useless variables into the model. Model specification involves selecting independent variables to include in the regression and the functional form of the regression equation. Omission of a relevant variable s Inclusion of an unnecessary variable s Adopting the wrong functional form Errors of measurement Incorrect specification of the stochastic.

Lets consider the multiple linear regression model. Redundant predictors lead to problems such as inflated standard errors for the regression coefficients Regression models that are overspecified yield unbiased regression coefficients unbiased predictions of the response and an unbiased MSE. Consider again the estimated regression equation.

We say that a model is misspecified when it violates the assumptions underlying linear regression its functional form is incorrect or it contains time series specification problems. Our discussion here can be easily generalized to more than two regressors. Ramseys 1969 regression specification error test RESET has proven to be useful in this regard.

Specification is the process of developing the statistical model in a regression analysis. Consider the model below. This can result in inflated errors for regressors and can distort the estimated coefficients.

We are interested in estimating the causal effect of class size on test score. In particular bias the expected value of the difference of an estimated parameter and the true underlying value occurs if an independent variable is correlated with the errors inherent in the underlying process. In a narrower sense the specification error refers to explanatory variables.

ˆT estScore 6860 87 110 043 size 0650 0031 english. Up to 10 cash back There are two basic types of specification errors. The first misspecification test under evaluation is the Ramsey RESET Regression Equation Specification Error Test test which does not require any information on.

In statistics errors-in-variables models or measurement error models are regression models that account for measurement errors in the independent variables. BIt detects the presence of dummy variables in a regression model. As such those models account only for errors in the dependent variables or responses.

Regression Tutorial With Analysis Examples Statistics By Jim

Types Of Reviews In Software Testing Software Testing Software Development Life Cycle Testing Techniques

Destructive Testing Complete Guide Software Testing Testing Strategies Teaching Coding

2

Taxonomy Of Software Testing Concept Download Scientific Diagram Taxonomy Software Testing Diagram

Pin On Qa

Going Deeper Into Regression Analysis With Assumptions Plots Solutions Regression Analysis Regression Analysis

Introductory Biostatistics Ebook Science Textbook Digital Book Textbook

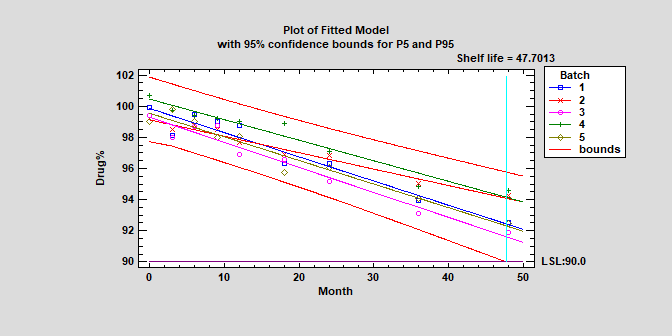
Regression Analysis Examples Of Regression Models Statgraphics

Model Misspecification An Overview Sciencedirect Topics

Simple Linear Regression

Pin On Test Planning And Methodology

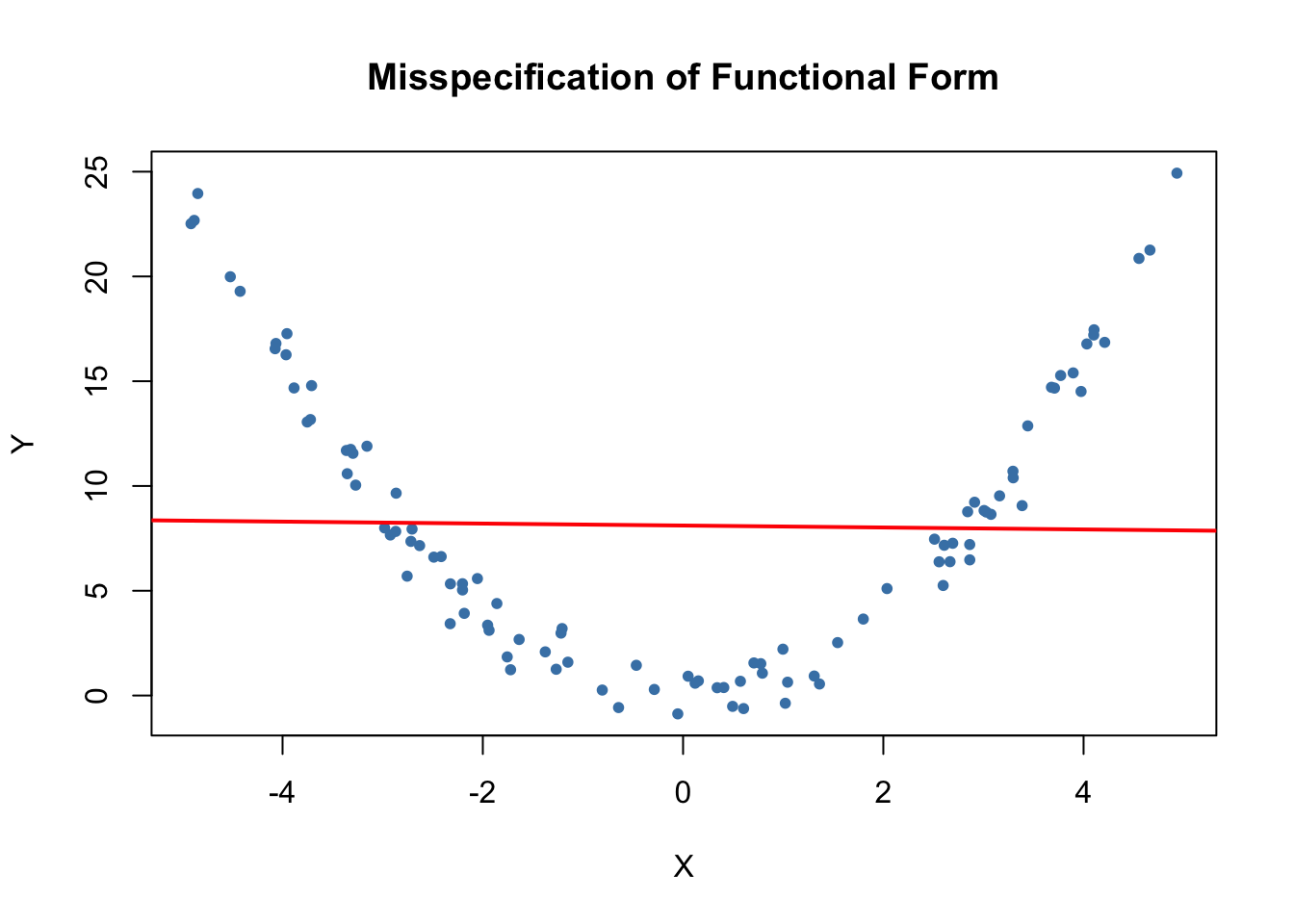
9 2 Threats To Internal Validity Of Multiple Regression Analysis Introduction To Econometrics With R

Lecture 9 Model Specification Youtube

Uopwcdglgfpmim

Model Specification Choosing The Correct Regression Model Statistics By Jim

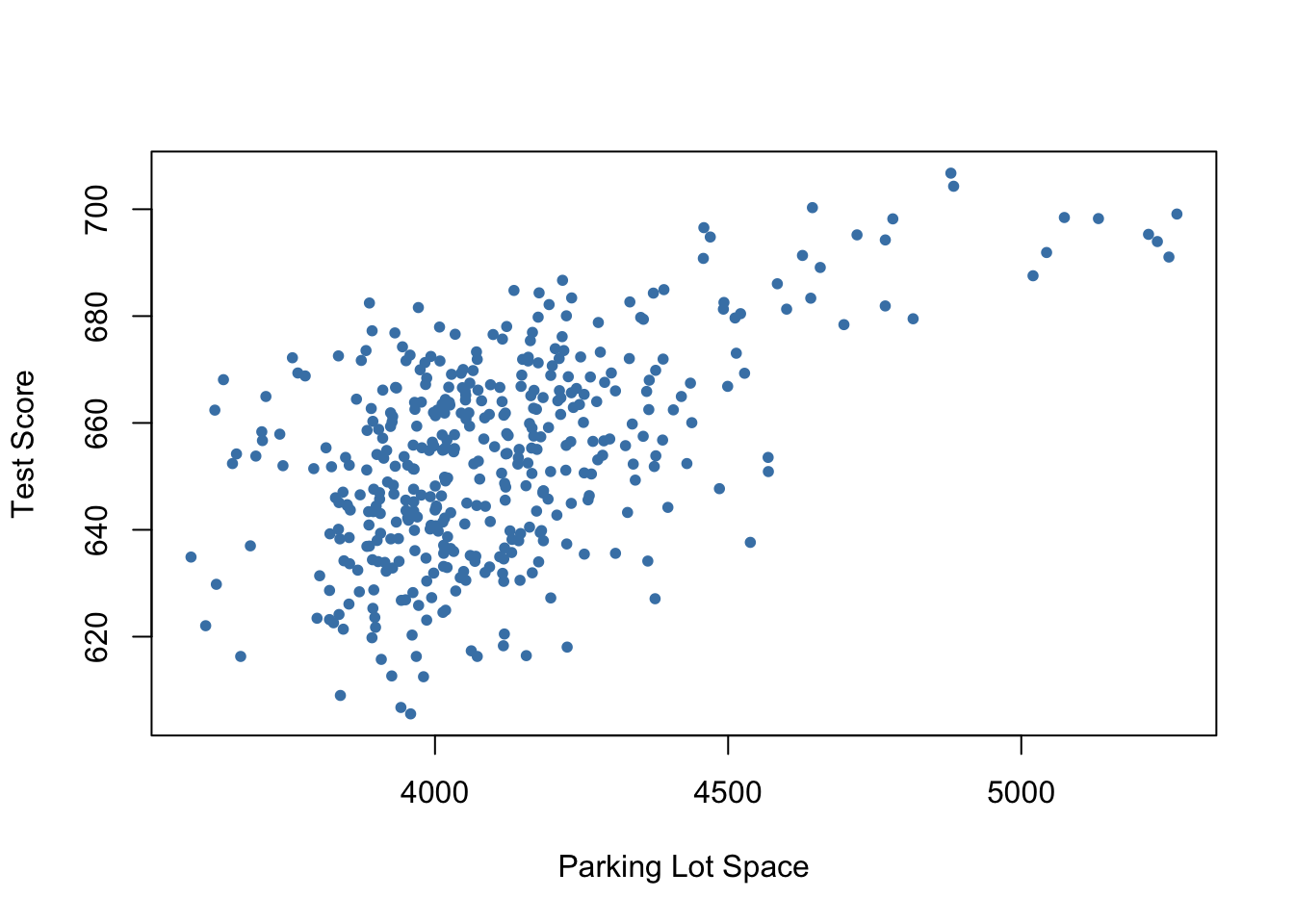
7 5 Model Specification For Multiple Regression Introduction To Econometrics With R

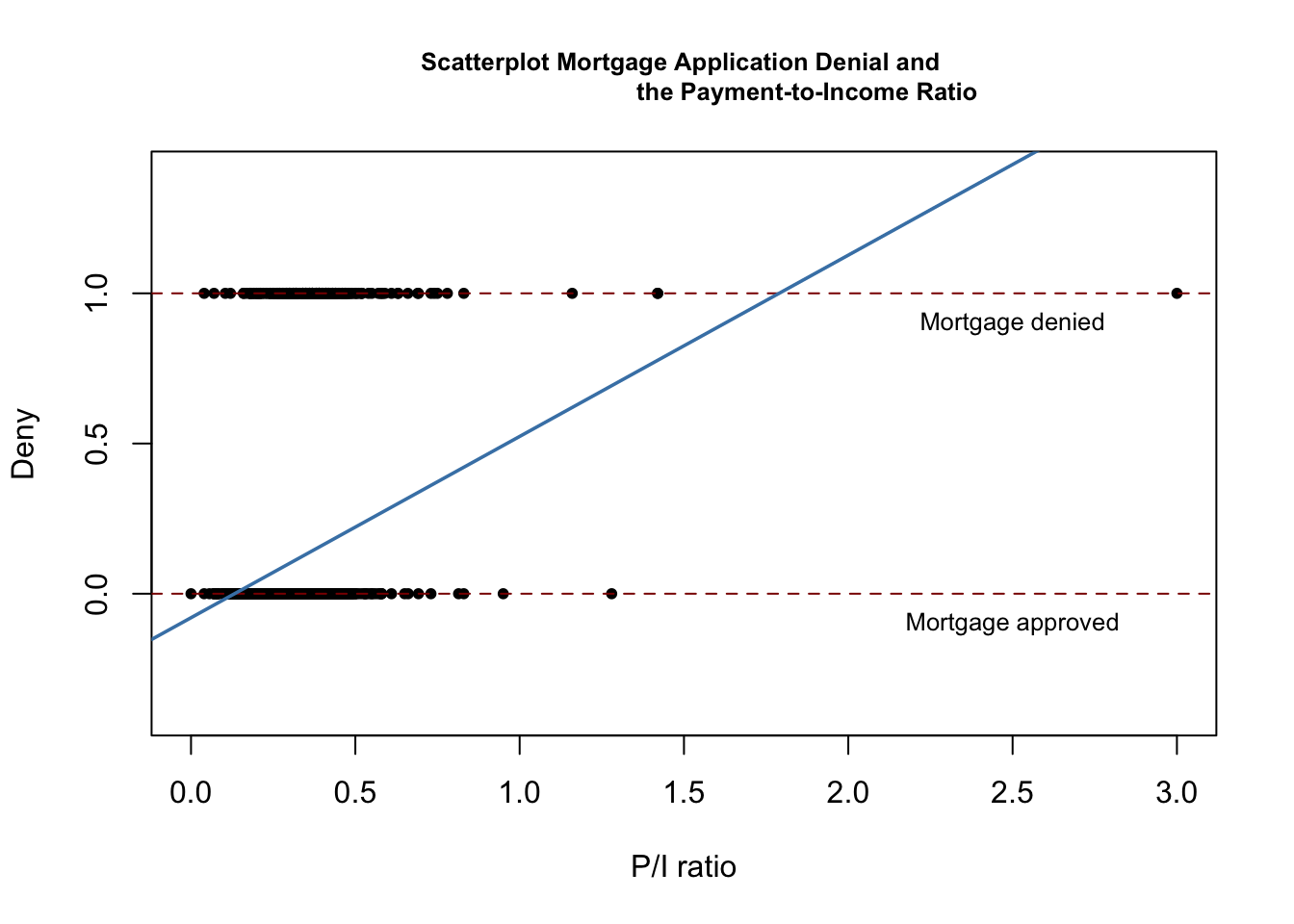
11 1 Binary Dependent Variables And The Linear Probability Model Introduction To Econometrics With R

Model Specification In Regression Analysis Springerlink